 |
|
Laboratorio di MATLAB |
1. Funzioni In Matlab una funzione f : R ® R può essere rappresentata in più modi:
- mediante una coppia di vettori ( x, y ), dove x = [ x1 ... xn ] è un vettore arbitrario di numeri reali ed y = f( x ) = [ f( x1 ) ... f( xn ) ], è il corrispondente vettore delle immagini;
- simbolicamente mediante una stringa, con la sintassi 'f(x)';
- mediante un m-file.
1.1 Funzioni elementari. In Matlab sono predefinite varie funzioni elementari, alcune delle quali sono riportate qui di seguito:
| funzione esponenziale: exp( x ) logaritmo naturale: log( x ) radice quadrata (square root): sqrt( x ) seno: sin( x ) coseno: cos( x ) tangente: tan( x ) arcoseno: asin( x ) arcocoseno: acos( x ) arcotangente: atan( x ) seno ipebolico: sinh( x ) coseno iperbolico: cosh( x ) tangente iperbolica: tanh( x ) arcoseno iperbolico: asinh( x ) arcocoseno iperbolico: acosh( x ) funzione segno: sign( x ) funzione pavimento: floor( x ) funzione soffitto: ceil( x ) |
Dato un vettore x in entrata, ognuna di queste funzioni restituisce il vettore delle immagini in unscita.
Ø Il segno sign( x ) di un numero reale x é + 1 se x é positivo, 0 se x = 0, - 1 se x é negativo. Ad esempio sign( f( x ) ) é il segno della funzione f.
Ø Il pavimento floor( x ) di un numero reale x é il piu' grande intero minore o uguale ad x, mentre il soffitto ceil( x ) di x é il piu' piccolo intero maggiore o uguale ad x. Ad esempio si ha
| floor( 1 / 2 ) = 0, floor( - 1 / 2 ) = - 1, floor( 3 / 2 ) = 1, floor( - 3 / 2 ) = - 2, floor( pi ) = 3, floor( - pi ) = - 4, floor( e ) = 2, floor( sqrt( 2 ) ) = 1, |
ceil( 1 / 2 ) = 1, ceil( - 1 / 2 ) = 0, ceil( 3 / 2 ) = 2, ceil( - 3 / 2 ) = - 1, ceil( pi ) = 4, ceil( - pi ) = - 3, ceil( e ) = 3, ceil( sqrt( 2 ) ) = 2. |
Per l'elenco completo delle funzioni elementari predefinite in Matlab, si consulti l'help di linea relativo alle Elementary math functions (utilizzando la finestra Help / Help Window, oppure utilizzando direttamente il comando help elfun).
1.2 Operazioni tra funzioni.1.2.1 Produtto di uno scalare per una funzione. Il prodotto di uno scalare l ÎR per una funzione f : R ® R è la funzione l f : R ® R definita ponendo per ogni x ÎR
( l f )( x ) = l f( x ).
In Matlab: l f( x )
1.2.2 Somma e differenza di funzioni. La somma di due funzioni reali f : R ® R e g : R ® R è la funzione f + g : R ® R definita ponendo per ogni x ÎR
( f + g )( x ) = f( x ) + g( x ).
In Matlab: f( x ) + g( x ), f( x ) - g( x ).
1.2.3 Prodotto e quziente di funzioni. Il prodotto ed il quoziente di due funzioni f : R ® R e g : R ® R sono le funzioni f g : R ® R ed f/g : R ® R definite rispettivamente ponendo per ogni x ÎR
( f g )( x ) = f( x ) g( x )
( f / g )( x ) = f( x ) / g( x ).
In Matlab: f( x ) .* g( x ), f( x ) ./ g( x ).1.2.4 Composizione di funzioni. Date due funzioni f : R ® R e g : R ® R, la funzione composta f ° g : R ® R è definita ponendo per ogni x ÎR
( f ° g )( x ) = f( g( x ) ).
In Matlab: f( g( x ) ).1.2.5 Funzioni esponenziali. Date due funzioni f : R ® R e g : R ® R, la funzione fg : R ® R è definita ponendo per ogni x ÎR
( fg )( x ) = f( x )g( x ).
In Matlab: f( x ).^g( x ).
1.3 Rappresentazione grafica di una funzione. La rappresentazione grafica di funzione dipende dal modo in cui la funzione è rappresentata.
1.3.1 Il comando plot. Dati due vettori x = [ x1 ... xn ] e y = [ y1 ... yn ], il comando plot( x, y ) disegna, in una finestra grafica, la linea spezzata che collega i punti di coordinate ( x1, y1 ), ..., ( xn, yn ).
Ø Possiamo rappresentare nella finestra grafica di Matlab il quadrato di vertici
A = ( 1, 0 ), B = ( 2, 1 ), C = ( 1, 2 ), D = ( 0, 1 ),
utilizzando le istruzioni:
» x = [ 1 2 1 0 1 ]; y = [ 0 1 2 1 0 ]; plot( x, y )
In particolare, possiamo rappresentare solo i quattro vertici mediante (ad esempio) un asterisco con le istruzioni:
» x = [ 1 2 1 0 1 ]; y = [ 0 1 2 1 0 ]; plot( x, y, '*' )
Se invece vogliamo rappresentare i quattro vertici con un asterisco ed i lati che li collegano, allora si utilizzano le istruzioni:
» x = [ 1 2 1 0 1 ]; y = [ 0 1 2 1 0 ]; plot( x, y, '-*' )
In Matlab si può rappresentare il grafico di una funzione utilizzando il comando plot. Per far questo bisogna rappresentare la funzione come un vettore formato dai valori che essa assume su un numero finito di punti.
Per approssimare una funzione f su un intervallo [ a, b ], si può procedere nel modo seguente:
- si suddivide l'intervallo [ a, b ] in t + 1 punti equispaziati (in corrispondenza dei quali si valuterà la funzione); questo corrisponde alla costruzione del vettore x = [ a : D : b ], formato dai punti a, a + D, a + 2 D, a + 3 D, ..., a + t D = b, dove D = ( b - a ) / t è il passo;
- si costruisce il vettore y delle immagini dei punti contenuti nel vettore x, ponendo y = f( x );
- si disegna la funzione mediante il comando plot( x, y ).
Ø Per disegnare la funzione seno tra 0 e 2p, si può scrivere:» x = [ 0 : 2*pi / 1000 : 2*pi ]; y = sin(x); plot(x,y)
Per rappresentare più funzioni nella stessa finestra grafica si può usare ancora il comando plot, nel modo seguente:
- si definisce il vettore x = a : t : b;
- si definiscono i vettori delle immagini
y1 = f1( x ); y2 = f2( x ); ... yn = fn( x );
- si disegnano le curve: plot( x, y1, x, y2, ..., x, yn ).
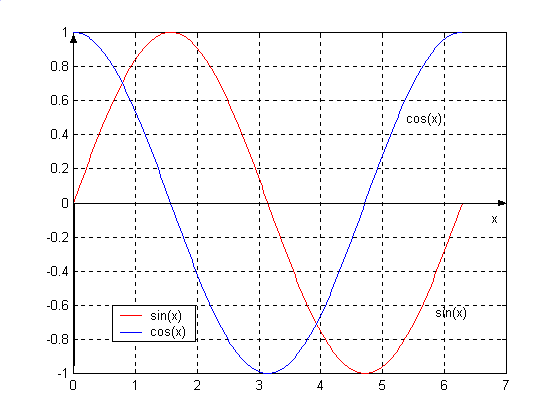
Ø Con le istruzioni
» x = [ 0 : 2*pi / 1000 : 2*pi ];
» y1 = sin( x ); y2 = cos( x );
» plot( x, y1, x, y2)si rappresentano, in colori diversi, il seno ed il coseno tra 0 e 2p.
 |
Invece con le istruzioni
» x = [ 0 : 2*pi / 1000 : 2*pi ];
» y1 = sin( x ); y2 = cos( x );
» plot( x, y1, ':', x, y2, '--')si ottengono i grafici delle due curve tratteggiati in modo differente. Si possono anche rappresentare solo i punti senza alcuna linea di raccordo: ad esempio con le istruzioni
» x = [ 0 : 2*pi / 100 : 2*pi ];
» y1 = sin( x ); y2 = cos( x );
» plot( x, y1, 'r*', x, y2, 'g+')si disegnano i punti che rappresentano il seno mediante asterischi rossi (r = red), e disegna i punti che rappresentano il coseno mediante + verdi (g = green).
Ø Il comando grid permette di visualizzare una graglia di riferimento:
» x = [ 0: 2*pi/1000 : 2*pi ]; y = sin(x); plot( x, y ), grid on
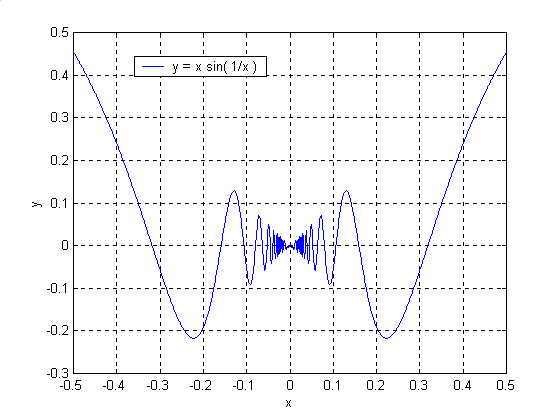
Ø Con le seguenti istruzioni si disegna il grafico della funzione f : R ® R definita da f( x ) = x sin( 1/x ), sull'intervallo [ - 0.5, 0.5 ]:
» x = -0.5 : 0.001 : 0.5;
» y = x.*sin( 1./x );
Warning: Divide by zero.
» plot( x, y )
 |
1.3.2 Il comando fplot. Per rappresentare il grafico di una funzione si può anche utilizzare il comando fplot. La sintassi di questo comando è
fplot( 'expr', [ a, b ] )
dove 'expr' è l'espressione simbolica di una funzione, ed [a , b ] è l'intervallo su cui si vuole rappresentare la funzione. Poiché expr è una stringa, deve essere racchiusa tra apici.
Ad esempio, per tracciare il grafico di x2 sull'intervallo [ - 1, 1 ], si scrive fplot( 'x^2', [ -1, 1 ] ). Il primo argomento di fplot è il polinomio scritto in forma simbolica (e racchiuso tra apici, essendo una stringa), mentre il secondo argomento è l'intervallo su cui si vuole tracciare il grafico.
Ø Per confrontare graficamente la funzione f( x ) = xx con la funzione g( x ) = x, sull'intervallo [ 0, 2 ], si può utilizzare il comando:
» fplot( '[ x^x, x ]', [ 0, 2 ] )
che genera il diagramma seguente, dal quale si vede che xx tende ad 1 al tendere di x a 0+ e che f( x ) ³ g( x ) per ogni x Î [ 0, 2 ].
1.4 Funzioni definite dall'utente. In Matlab si ha la possibilità di definire nuove funzioni mediante gli m-file. Un m-file è un file, con estensione m, che contiene una successione di comandi che possono essere interpretati ed eseguiti da Matlab. Gli m-file che definiscono una funzione sono chiamati file di funzione. In questi file tutte le variabili sono locali (contrariamente a quanto accade nei file script). Ogni file di funzione deve iniziare con la seguente sintassi:
function [ variabili di output ] = nome_funzione( variabili di input )
La parola function è l'identificatore che definisce l'm-file come file di funzione. Le variabili di output vanno racchiuse tra parentesi quadre (l'output è in generale un vettore), mentre le variabili di input vanno racchiuse tra parentesi tonde nell'usuale notazione funzionale. Il nome della funzione (nome_funzione) deve essere uguale al nome dell'm-file che la definisce. Si tenga presente che Matlab distingue tra lettere maiuscole e minuscole. In una sessione di Matlab la funzione può essere chiamata semplicemente scrivendone il nome.
Ø Si consideri la funzione di Riemann f : R ® R definita dalla seguente serie
|
f( x ) = |
|
|
Si dimostra che questa funzione è ben definita ed è continua su tutto R, ma non è derivabile in quasi alcun punto. Qui ci proponiamo semplicemente di rappresentare il grafico approssimativo di tale funzione. Poiché f è definita come una serie infinita, ci limiteremo a calcolare i primi n termini della somma. Definiamo f mediante il seguente m-file
function y = riemannfz( n, x )
t = 0;
for k = 1 : n
t = t + sin( k^2*pi*x ) / k^2;
end
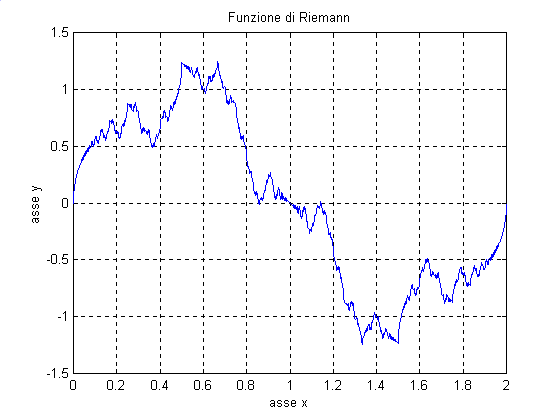
y = te quindi rappresentiamola sull'intervallo [ 0, 2 ] con le seguenti istruzioni
» x = 0 : 1/1000 : 2;
» y = riemannfz( 1000, x );
» plot( x, y ), grid onSi ottiene così il grafico seguente
 |
1.5 Zeri di una funzione. Per trovare gli zeri di una funzione si può utilizzare il comando fzero, che ha la sintassi fzero( expr, x0 ), dove expr è la stringa che definisce la funzione. Questo comando restituisce un valore prossimo ad x0 in cui la funzione si annulla. Tuttavia, questo comando determina solo i punti in cui la funzione attraversa l'asse delle ascisse; quindi non determina i punti in cui la funzione è tangente all'asse x.
In genere conviene disegnare il grafico della funzione per determinare la posizione degli eventuali zeri, e poi utilizzare il comando fzero per ottenere una loro stima più precisa.Ø Cerchiamo gli zeri della funzione f( x ) = x + 2 e-x - 3, sull'intervallo [ -1, 5 ]. Iniziamo col disegnare il grafico di f sull'intervallo dato:
» x = -1 : 0.001 : 5;
» y=x+2*exp(-x)-3;
» plot(x,y), grid onEsaminando il grafico ottenuto si vede che f presenta due zeri in prossimita di x = -0.5 e di x = 2.8. Utilizziamo il comando fzero per ottenere un risultato più preciso:
» fzero('x+2*exp(-x)-3',-.5)
Zero found in the interval: [-0.38686, -0.61314].
ans =
-0.5831
» fzero('x+2*exp(-x)-3',2.8)
Zero found in the interval: [2.688, 2.912].
ans =
2.88871.5 Minimi di una funzione. Per trovare i minimi di una funzione si può utilizzare il comando fmin, che ha la sintassi fmin( expr, x1, x2 ), dove expr è la stringa che definisce la funzione. Questo comando restituisce un valore che rende minima la funzione nell'untervallo [ x1, x2 ]. Occorre però utilizzare questo comando con cautela. L'algoritmo sottostante questo comando inizia col cercare il primo punto di minimo in corrispondenza del quale la pendenza della funzione è nulla. Se ne trova uno allora termina, altrimenti esamina i valori che la funzione assume agli estremi dell'intervallo. Quindi il comando fmin da una risposta sbagliata quando la funzione possiede più punti di minimo a tangente orizzontale ed il primo minimo non è assoluto, oppure quando la funzione possiede almeno un punto di minimo a tangente orizzontale, ma assume il suo valore minimo in un estremo dell'intervallo. Conviene sempre disegnare il grafico della funzione per controllare che i risultati siano corretti.
Ø Consideriamo la funzione f( x ) = x sin x sull'intervallo [ 0, 4 p ]. Allora utilizzando il comando fmin si ha
» fmin('x*sin(x)',0,4*pi)
ans =
4.9132Tuttavia, con le istruzioni
» fplot('x*sin(x)',[0,4*pi])
» grid onsi ottiene il grafico
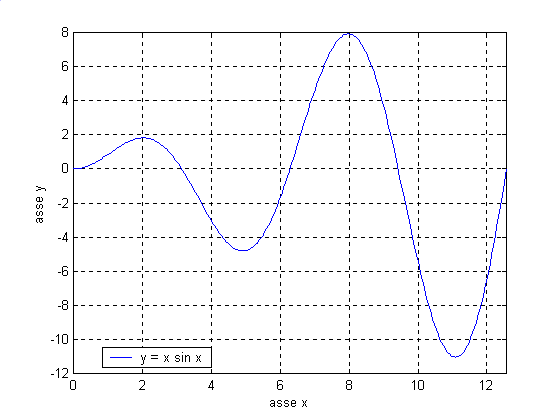 |
dal quale si vede che la funzione in x = 4.9132 presenta solo un minimo locale e che assume invece il suo valore minimo nell'intervallo [ 10, 12 ]. A questo punto, quindi, possiamo determinare il vero minimo della funzione:
» fmin('x*sin(x)',10,12)
ans =
11.0856Consideriamo ancora la funzione f( x ) = x sin x, ma sull'intervallo [ 0, 10 ]. Ancora si ha
» fmin('x*sin(x)',0,10)
ans =
4.9132Tuttavia, come si vede dal grafico, il f assume il suo valore minimo nel secondo estremo dell'intervallo, ossia in x = 10:
» 4.9132*sin(4.9132)
ans =
-4.8145» 10*sin(10)
ans =
-5.4402Osservazione Per trovare i massimi della funzione f( x ) basta trovare i minimi della funzione - f( x ). Anche in questo caso si può utilizzare il comando fmin.
2. Esercizi Ø Disegnare il grafico delle funzioni pavimento e soffitto sull'intervallo [ - 2, 2 ].
Soluzione:» x = [ -2: 1/1000 : 2 ];
» y1 = floor( x ); y2 = ceil( x );
» plot( x, y1, x, y2 )Ø Rappresentare graficamente l'arcotangente tra - 10 e 10.
Soluzione:» x = - 10 : .0001 : 10; y = atan( x ); plot( x, y )
Ø Rappresentare graficamente la funzione f : [ -1, 3 ] ® R definita da
f( x ) = ex sin x.
Soluzione:
» x = [ -1 : 0.1 : 2 ]; y = exp(x).*sin(x); plot( x, y )
Ø Disegnare il grafico del segno della funzione f( x ) = x^5 - 3 x^2 - x + 2 sull'intervallo [ 0, 1 ].
Soluzione:» x = [ 0: 1/1000 : 1 ];
» y = sign( x.^5 - 3* x.^2 - x + 2 );
» plot( x, y )Ø Disegnare il grafico della funzione g( x ) = x^2 sin( 1 / x ), sull'intervallo [ -0.5, 0.5 ].
Soluzione:» x = [ -.5: 1/1000 : .5 ]; y = x.^2.*sin(1./x); plot( x, y )
ØTracciare contemporaneamente il grafico dei due polinomi seguenti x4 - 5 x2 + 4 e x^2 - 1, sull'intervallo [ - 3, 3 ], utilizzando il comando fplot.
Soluzione:» fplot( '[ x^4-5*x^2+4, x^2 ]', [ -3, 3 ] )
Ø Studiare la funzione f(x) = ( 1 - x3 )1/3, sull'intervallo [ -2, 2 ].
Soluzione:
x=-2:1/1000:2; y=(1-x.^3).^(1/3); plot(x,y), grid on
Ø Studiare la funzione f(x) = x ln | x |, sull'intervallo [ -2, 2 ].
Soluzione:
» x=-2:1/1000:2; y=x.*log(abs(x)); plot(x,y), grid on
Ø Studiare la funzione f(x) = x exp( - x2 ), sull'intervallo [ -4, 4 ]. In particolare determinarne i massimi ed i minimi.
Ø Studiare la funzione
|
x ( x2 - 1 ) ( x2 - 4 ) |
|
| f( x ) = |
---------------------------- |
|
x4 + 1 |
sull'intervallo [ -4, 4 ]. In particolare determinarne i massimi ed i minimi.
Ø Definire un file di funzione per la funzione doppiamente esponenziale
|
E( x ) = |
|
|